Difference between revisions of "Draft Standards for Post-Calculation Health Reports"
John Chodera (talk | contribs) |
|||
| (32 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
This page contains a discussion regarding a draft standard practice for analyses to be run following an alchemical free energy calculation to provide a "health report" indicating the quality of an alchemical free energy calculations, and identifying some common modes of failure generally known to occur in these types of calculations. The hope is to begin a community discussion on this topic so that multiple implementations of these standard checks will be available for different popular codes. | This page contains a discussion regarding a draft standard practice for analyses to be run following an alchemical free energy calculation to provide a "health report" indicating the quality of an alchemical free energy calculations, and identifying some common modes of failure generally known to occur in these types of calculations. The hope is to begin a community discussion on this topic so that multiple implementations of these standard checks will be available for different popular codes. | ||
| − | = Division of simulation data into "equilibrated region" and "production analysis region" = | + | = Standard steps for post-simulation analysis = |
| + | |||
| + | == Division of simulation data into "equilibrated region" and "production analysis region" == | ||
While a Markov chain Monte Carlo simulation does not require that any initial "equilibration" region be identified and discarded to achieve asymptotically consistent results (see Charles Geyer's discussion [http://users.stat.umn.edu/~geyer/mcmc/burn.html Burn-In is Unnecessary]), the initial starting configuration and box volumes for an alchemically free energy calculation are often so highly atypically samples from the equilibrium distribution that failing to discard some initial transients of relaxation to equilibrium will lead to highly biased free energy estimates. | While a Markov chain Monte Carlo simulation does not require that any initial "equilibration" region be identified and discarded to achieve asymptotically consistent results (see Charles Geyer's discussion [http://users.stat.umn.edu/~geyer/mcmc/burn.html Burn-In is Unnecessary]), the initial starting configuration and box volumes for an alchemically free energy calculation are often so highly atypically samples from the equilibrium distribution that failing to discard some initial transients of relaxation to equilibrium will lead to highly biased free energy estimates. | ||
| Line 11: | Line 13: | ||
This should be done for each "leg" of the alchemical free energy simulation thermodynamic cycle. | This should be done for each "leg" of the alchemical free energy simulation thermodynamic cycle. | ||
| − | == Manual inspection of key properties == | + | === Manual inspection of key properties === |
If properties of the simulation are to be inspected manually (which is not recommended, but may be useful for graphical illustration), the practitioner is advised to examine the following properties: | If properties of the simulation are to be inspected manually (which is not recommended, but may be useful for graphical illustration), the practitioner is advised to examine the following properties: | ||
| − | === Box volume === | + | ==== Box volume ==== |
Many simulation preparation schemes for explicit solvent simulations utilize a scheme that replicates a small equilibrated water box (potentially generated with a different solvent or a different set of nonbonded simulation cutoffs or dispersion corrections), places the complex or ligand within this box, and then culls waters with significant overlap with the solute molecules. Counterions are added through one of several heuristic schemes. This process can lead to initial solvent densities that significantly different densities than the average equilibrium density, where density deviations of even 0.1% are highly significant and can result in enormous artificial pressure deviations. | Many simulation preparation schemes for explicit solvent simulations utilize a scheme that replicates a small equilibrated water box (potentially generated with a different solvent or a different set of nonbonded simulation cutoffs or dispersion corrections), places the complex or ligand within this box, and then culls waters with significant overlap with the solute molecules. Counterions are added through one of several heuristic schemes. This process can lead to initial solvent densities that significantly different densities than the average equilibrium density, where density deviations of even 0.1% are highly significant and can result in enormous artificial pressure deviations. | ||
| Line 29: | Line 31: | ||
'''TODO: Show examples''' | '''TODO: Show examples''' | ||
| − | === | + | ==== Hydrogen bonding ==== |
| − | For a standard simulation sampling from a single thermodynamic state, the ''reduced potential'' is given by | + | Hydrogen bonds within a system often equilibrate substantially more slowly than other properties. For example, hydrogen bonding between a ligand and binding-site water, between a receptor and surrounding water, and perhaps sometimes even between the ligand and receptor itself, can be slow to reach their equilibrium values. In many cases, timescales for this equilibration in the number of hydrogen bonds to water, for example, can be substantially slower than timescales for apparent equilibration of the system potential energy, for example. |
| + | |||
| + | ==== Reduced potential ==== | ||
| + | |||
| + | For a standard simulation sampling from a single thermodynamic state, the [[Multistate_Bennett_Acceptance_Ratio#Reduced_potential|''reduced potential'']] is given by | ||
: <math>u(x_t) = - \ln \pi(x_t) + c</math> | : <math>u(x_t) = - \ln \pi(x_t) + c</math> | ||
where <math>\pi(x)</math> represents the normalized probability density for the MCMC simulation, <math>x_t</math> is the sampled simulation state of the system at time index <math>t</math> (which may include positions, velocities, box vectors, etc.), and <math>c</math> is an arbitrary additive constant. | where <math>\pi(x)</math> represents the normalized probability density for the MCMC simulation, <math>x_t</math> is the sampled simulation state of the system at time index <math>t</math> (which may include positions, velocities, box vectors, etc.), and <math>c</math> is an arbitrary additive constant. | ||
| Line 46: | Line 52: | ||
: [[File:hamiltonian-exchange-reduced-potential.png]] | : [[File:hamiltonian-exchange-reduced-potential.png]] | ||
| − | == Automated equilibration determination == | + | === Automated equilibration determination === |
It is highly recommended that an automated method instead be employed for dividing the simulation history into "unequilibrated" and "equilibrated" regions, though manual inspection of the properties suggested to verify the automated scheme has correctly divided the simulation is often a good visual check of simulation quality. | It is highly recommended that an automated method instead be employed for dividing the simulation history into "unequilibrated" and "equilibrated" regions, though manual inspection of the properties suggested to verify the automated scheme has correctly divided the simulation is often a good visual check of simulation quality. | ||
| Line 54: | Line 60: | ||
'''It is recommended that the production region of the simulation trajectory be defined as the interval that terminates at the end of the simulation and begins at the time which maximizes the number of uncorrelated samples in that interval.''' | '''It is recommended that the production region of the simulation trajectory be defined as the interval that terminates at the end of the simulation and begins at the time which maximizes the number of uncorrelated samples in that interval.''' | ||
This scheme is a simpler form of [http://dx.doi.org/10.1063/1.1638996 one suggested by Wei Yang that requires statistical assumptions of normality]. | This scheme is a simpler form of [http://dx.doi.org/10.1063/1.1638996 one suggested by Wei Yang that requires statistical assumptions of normality]. | ||
| − | To implement such a scheme, several equally-spaced origins <math>t_0</math> of the simulation interval are considered, and the number of uncorrelated configurations in the intervals <math>[t_0, T]</math> are computed, where <math>T</math> denotes the end of the simulation. | + | To implement such a scheme, several equally-spaced origins <math>t_0</math> of the simulation interval are considered, and the number of uncorrelated configurations in the intervals <math>[t_0, T]</math> are computed, where <math>T</math> denotes the end of the simulation. (DLM: We have found that in some cases this seems to lead us astray; I've asked P. Klimovich who did this work to comment on this with details.) |
| − | For each interval, the number of effectively uncorrelated configurations <math>N_{eff}</math> is given by | + | |
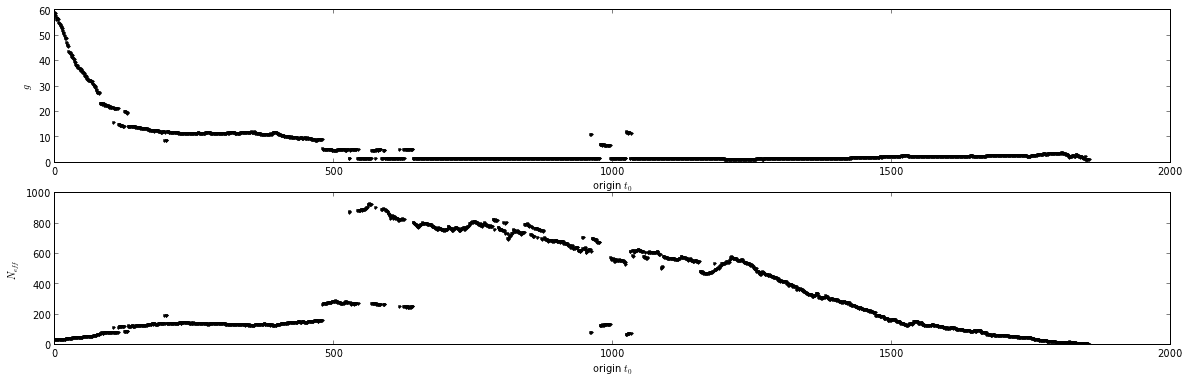
| − | : <math>N_{eff} = (T - t_0 + 1) / g</math> | + | For each interval, the number of effectively uncorrelated configurations <math>N_{eff}</math> is given by: <math>N_{eff} = (T - t_0 + 1) / g</math> |
| − | where <math>g = 1 + 2 \tau</math> is the statistical inefficiency computed for the interval <math>[t_0, T]</math>, with <math>\tau</math> denoting the integrated autocorrelation time computed over that interval. | + | where <math>g = 1 + 2 \tau</math> is the statistical inefficiency computed for the interval <math>[t_0, T]</math>, with <math>\tau</math> denoting the integrated autocorrelation time computed over that interval. |
An example of this for a Hamiltonian-exchange simulation can be seen here: | An example of this for a Hamiltonian-exchange simulation can be seen here: | ||
| Line 64: | Line 70: | ||
The maximum of <math>N_{eff}</math> represents the best choice of <math>t_0</math>, the beginning of the production region. | The maximum of <math>N_{eff}</math> represents the best choice of <math>t_0</math>, the beginning of the production region. | ||
| − | + | Note that a robust scheme for estimating the integrated autocorrelation time / statistical inefficiency must be used, and these results will depend somewhat on that choice in tricky examples. The [http://github.com/choderalab/pymbar pymbar] package contains a ''timeseries'' module that may be useful for this purpose. A robust scheme is described in [http://dx.doi.org/10.1021/ct0502864 Sections 2.4 and 5.2 of this JCTC paper], though FFT-based methods can be much faster. | |
| + | |||
| + | The statistical inefficiency <math>g</math> should be computed for an appropriate property of the simulation. If there are structural relaxation times known to be critical, these should be evaluated and the ''maximum'' statistical inefficiency over these considered as the effective statistical inefficiency of note. | ||
| − | '''If obvious structural relaxation times are not available, the appropriate time-dependent quantity to use for computation of the statistical inefficiency <math>g</math> is the reduced potential---the negative logarithm of the unnormalized probability density.''' | + | '''If obvious structural relaxation times are not available, the appropriate time-dependent quantity to use for computation of the statistical inefficiency <math>g</math> is the reduced potential---the negative logarithm of the unnormalized probability density.''' But note that in practice, apparent correlation times in the reduced potential may be much lower, especially in explicit solvent, due to the fraction of the system consisting of solvent. Hence, it is especially important to use the '''maximum''' relaxation time among important observables. |
| + | (MRS: In that case, what about the total energy - (water-water) energy? Not always available, but does avoid the problem you mention. Another quantity is dH/dlambda) | ||
| − | = Number of uncorrelated samples = | + | == Number of uncorrelated samples == |
While only a rule of thumb, '''we suggest the equilibrated production region contain at least 20 statistically uncorrelated samples per thermodynamic state'''. | While only a rule of thumb, '''we suggest the equilibrated production region contain at least 20 statistically uncorrelated samples per thermodynamic state'''. | ||
If fewer samples are obtained, the statistical error estimate of methods like [[Bennett_Acceptance_Ratio|BAR]] and [[Multistate_Bennett_Acceptance_Ratio|MBAR]] will be unreliable. | If fewer samples are obtained, the statistical error estimate of methods like [[Bennett_Acceptance_Ratio|BAR]] and [[Multistate_Bennett_Acceptance_Ratio|MBAR]] will be unreliable. | ||
| − | = Verifying acceptable alchemical state overlap = | + | == Verifying acceptable alchemical state overlap == |
| − | It is critical that the alchemical states (or, more generally, thermodynamic states) simulated have sufficient phase space overlap to connect the two endstates of interest. Poor overlap is the reason many simulations fail, introducing large biases or errors into the computed results. Data analysis techniques like [[Thermodynamic_Integration|TI]], [[Bennett_Acceptance_Ratio|BAR]], or [[Multistate_Bennett_Acceptance_Ratio|MBAR]] may not clearly indicate that phase space overlap is poor without additional computation (though slow convergence of MBAR is often a sign of poor overlap). | + | It is critical that the alchemical states (or, more generally, thermodynamic states) simulated have sufficient phase space overlap to connect the two endstates of interest. Poor overlap is the reason many simulations fail, introducing large biases or errors into the computed results. Data analysis techniques like [[Thermodynamic_Integration|TI]], [[Bennett_Acceptance_Ratio|BAR]], or [[Multistate_Bennett_Acceptance_Ratio|MBAR]] may not clearly indicate that phase space overlap is poor without additional computation (though slow convergence of MBAR is often a sign of poor overlap, as is inconsistency between analysis techniques such as TI, BAR, and MBAR). |
'''We recommend that explicit steps be taken to ensure good phase space overlap between all simulated thermodynamic states.''' | '''We recommend that explicit steps be taken to ensure good phase space overlap between all simulated thermodynamic states.''' | ||
| Line 81: | Line 90: | ||
Several approaches can be used to verify this. | Several approaches can be used to verify this. | ||
| − | == Computation of the overlap matrix in MBAR == | + | === Computation of the overlap matrix in MBAR === |
Those using [[Multistate_Bennett_Acceptance_Ratio|MBAR]] to analyze simulations can utilize the calculation of the ''overlap matrix'' among alchemical states to verify whether there is sufficient overlap among states to ensure the graph of states is well-connected. | Those using [[Multistate_Bennett_Acceptance_Ratio|MBAR]] to analyze simulations can utilize the calculation of the ''overlap matrix'' among alchemical states to verify whether there is sufficient overlap among states to ensure the graph of states is well-connected. | ||
| Line 91: | Line 100: | ||
The larger the gap between the first and second largest eigenvalues of <math>{\bf O}</math>, the better connected all states are. A small gap or degenerate dominant eigenvalues indicates the states are poorly connected. | The larger the gap between the first and second largest eigenvalues of <math>{\bf O}</math>, the better connected all states are. A small gap or degenerate dominant eigenvalues indicates the states are poorly connected. | ||
| − | '''Michael Shirts: Can you fill in more about this issue?''' | + | '''Michael Shirts: Can you fill in more about this issue?''' The <math>i</math>th row of the <math>{\bf O}</math> matrix described the normalized probability of a given sample from the <math>i</math>th to have been generated in the <math>j</math>th state. For example, if all entries are equal, then the average sample from the <math>i</math>th state is equally likely to have been generated in all states, indicative of very high overlap. If only the diagonal element is populated, then it means that there is essentially no chance that sample could have come from any other state than the <math>i</math>th state, which is obviously very poor overlap. |
| + | |||
| + | |||
| + | (DLM: Also, we found that in some cases, picking a time to consider as "equilibrated" which minimizes g actually results in poorer overlap among states. MRS: does this comment belong here, or in a different section.) | ||
| + | |||
| + | === Pairwise computation of overlap with [[Bennett_Acceptance_Ratio|BAR]] === | ||
| + | |||
| + | In a similar manner to [[Multistate_Bennett_Acceptance_Ratio|MBAR]] above, elements of the overlap matrix <math>{\bf O} \equiv (o_{ij})</math> can be computed among those pairs of states for which data is available for a [[Bennett_Acceptance_Ratio|BAR]] computation is possible. The overlap matrix will be sparse, but its dominant eigenvalue gap can still be analyzed in a manner identical to that above with [[Multistate_Bennett_Acceptance_Ratio|MBAR]]. | ||
| + | |||
| + | (MRS: better to go directly to Bennett's paper, which which he shows there is a direct connection between the estimated uncertainty of the calculation and the overlap. So whether the overlap is enough is pretty much the same as asking whether the statistical uncertainty is low enough.) | ||
| + | |||
| + | === Replica-exchange acceptance probabilities === | ||
| + | |||
| + | In a standard replica-exchange simulation, exchanges are generally attempted only between pairs of replicas that are "neighbors" in some thermodynamically topological sense. (Note that [http://dx.doi.org/10.1063/1.3660669 recent work] has shown there are more efficient ways to conduct exchanges.) | ||
| + | |||
| + | '''In these simulations, examining the fraction of exchange attempts between neighbors that result in acceptance is a good way to tell if overlap is poor, as poor exchange acceptance probabilities is indicative of poor overlap.''' | ||
| + | |||
| + | Aside: Poor exchange rates will also indicate the benefit of replica exchange is not fully realized because of kinetic bottlenecks in the move through thermodynamic state space, hindering convergence. | ||
| + | Note that good neighbor exchange rates can be deceptive---it is only a necessary, but not sufficient, condition for convergence. | ||
| + | There are numerous cases where replicas still poorly mix globally even though it appears that all pairs of thermodynamic states have high exchange probabilities. | ||
| + | These issues are best diagnosed by looking at ''round-trip times'' between the two extreme states of interest. | ||
| + | Later sections cover this issue in more detai. | ||
| + | |||
| + | === Replica-exchange mixing statistics === | ||
| + | |||
| + | If a replica exchange simulation is performed using the recently-proposed [http://dx.doi.org/10.1063/1.3660669 Gibbs sampling] state mixing scheme, exchanges are attempted between replicas that are not simply "neighbors". This allows the construction of an empirical state-to-state transition matrix <math>T_{ij} = P(s_{t+1} = j | s_{t} = i)</math>, which represents the probability of observing a replica currently in state <math>i</math> in state <math>j</math> in the next iteration. This matrix can be constructed for "standard" replica exchange simulations as well, but will be banded tridiagonal. | ||
| + | |||
| + | We can analyze the "mixing statistics" of the equilibrated part of the simulation to ensure that the <math>(X,S)</math> chain is mixing reasonably well among the various alchemical states. | ||
| + | In practice, this is done by recording the number of times a replica transitions from alchemical state i to state j in a single iteration. We can use the fact that the overall chain must obey detailed balance to ensure all eigenvalues of the estimated transition matrix are real. | ||
| + | |||
| + | Note that if the subdominant eigenvalue would have been unity, then the chain would be decomposable, meaning that it completely separated into two separate sets of alchemical states that did not mix. This would have been an indication of poor phase space overlap between some alchemical states. | ||
| + | In practice, it's a great idea to monitor these statistics as the simulation is running, even if no data is discarded to equilibration at that point. They give not only a good idea of whether sufficient mixing is occurring, but it provides a lower bound on the mixing time in configuration space. | ||
| + | If the configuration x sampling is infinitely fast so that x can be considered to be at equilibrium given the instantaneous permutation S of alchemical state assignments, the subdominant eigenvalue <math>\lambda_2 \in [0,1]</math> gives an estimate of the mixing time of the overall <math>(X,S)</math> chain: | ||
| + | : <math> \tau_{eq} = \frac{1}{1 - \lambda_2} </math> | ||
| + | |||
| + | == Computation of statistical error == | ||
| + | |||
| + | '''To Do''' | ||
| + | |||
| + | (MRS: bootstrap turns out to be very useful. http://pubs.acs.org/doi/abs/10.1021/ct2003995 analyzes a bunch of different methods.) | ||
| + | |||
| + | Some discussion of block bootstrapping. | ||
| + | |||
| + | == Determining whether the calculation has converged == | ||
| + | |||
| + | === Block simulation analysis === | ||
| + | |||
| + | A common scheme for diagnosing convergence is to break the simulation into two or more statistically uncorrelated blocks and analyze these blocks independently. Concordance between estimates derived from each block is suggestive that the simulation has run long enough to converge, since each statistically independent subset acts like a statistical sample from the target density. | ||
| + | |||
| + | Care should be taken with this approach, as it is often difficult to decompose the simulation into blocks that are indeed statistically independent. This requires, at minimum, computation of the statistical inefficiency of the simulation to determine how far apart these blocks must be to be statistically uncorrelated. | ||
| + | |||
| + | Even then, it is difficult to ensure that no very long correlation times that are difficult to detect via a statistical inefficiency estimation procedure are in fact present. This test is to be regarded as a necessary, but not sufficient, test for convergence. | ||
| + | |||
| + | If a replica-exchange simulation is used, this test can still be performed, but subsequent sections enumerate more useful tests for convergence. | ||
| + | |||
| + | In general, we believe that block analysis is not nearly a strenuous enough test of convergence, and that analysis of replicate simulations from alternate starting structures is a far better means of accomplishing a similar end, as discussed in the following section.'''(DLM added this recommendation AGAINST this; is it OK with you?) | ||
| + | |||
| + | === Gelman-Rubin convergence criteria for replica-exchange simulations === | ||
| + | |||
| + | In 1992, Gelman and Rubin proposed a very clever idea for a convergence diagnostic in the case that multiple MCMC samplers are run from different initial sampler states [http://dx.doi.org/10.1214/ss/1177011136 DOI]. | ||
| + | |||
| + | The idea is simple: Each chain gives an individual estimate for some computed expectation or property, and the whole collection of chains give a (presumably more precise) estimate. These chains could be entirely separate sets of free energy calculations run from different starting structures, or different replicas within a replica exchange setup. We can simply compare the individual estimates to the overall estimate to determine whether the chains have been run long enough to see concordance between the individual and global estimates, to within appropriate statistical error. If not, then the samplers have not yet run long enough to sample all of the important modes of the density. | ||
| + | Considering the case of replica exchange, we can apply a similar idea, especially if we have initialized our replicas with different configurations (e.g. different docked ligand conformations, and potentially different protein conformations as well). | ||
| + | Let's first compute the global estimate of the free energy differences between thermodynamic states using all replicas: | ||
| + | (MRS: how do you calculate the free energy differences between state using only single replicas? I'm sure what "global" and "local" free energy differences are in this context. Confusing example) | ||
| + | : [[File:gelman-rubin.png]] | ||
| + | The global and replica estimates are shown with two standard errors (approximate 95% confidence intervals). If the simulation has converged, each nearly independent replica estimate should have a 5% of the replicas should be outside this interval. | ||
| + | We can turn these deviations into Z-scores: | ||
| + | : [[File:gelman-rubin-z-score.png]] | ||
| + | This could be used to formulate a statistical test for convergence. | ||
| + | |||
| + | '''We propose that replicas be initiated with different initial conformations (such as different ligand poses and/or protein models) and a Gelman-Rubin analysis performed to assess convergence.''' | ||
| + | |||
| + | === Comparison of multiple independent simulations === | ||
| + | |||
| + | == Detection of infrequent events coupled to the alchemical free energy == | ||
| + | |||
| + | Often, slow degrees of freedom can couple strongly to the quantities relevant to the estimation of the alchemical free energy difference (such as <math>\partial u/\partial \lambda</math> in TI or <math>\Delta u_{ij} \equiv u_j - u_i</math> in BAR/MBAR). We ''hope'' that this manifests itself in strong components of the correlation function integrated to estimate the statistical inefficiency, but this may not always happen. Instead, we can examine the simulation for degrees of freedom strongly coupled to these terms. | ||
| + | |||
| + | Here is an example of the slow torsional transitions of the sidechain of Val111, a residue lining the cavity binding site of T4 lysozyme L99A while binding to p-xylene: | ||
| + | : [[File:hindered-sidechain-torsion.png]] | ||
| + | (MRS: wouldn't the best way to find DoF coupled to TI would be to look at dh/dl? What does du/dl look like for these trajectories? Is that one step towards the automated approach?) | ||
| + | |||
| + | A more automated approach to detect these types of events is to examine the number of transitions for important structural features and ensure this is sufficient. For example, one can automatically count torsional transitions for sidechains around a ligand binding site, or torsions within a ligand. Whenever timescales are fast compared to the simulation time, or transition counts are high, it is reassuring. And whenever the number of transitions is zero, it may be because alternate conformations are extremely unfavorable. But, whenever transition counts are low but non-negligible (i.e. when timescales are long) it is a warning sign that further investigation may be needed. | ||
| − | == | + | == Detection of artifacts in the simulation parameters == |
| − | + | It is important to regularly validate your employed setup against standard results in test systems with known results, such as [http://www.escholarship.org/uc/item/6sd403pz hydration free energies], and ideally binding free energies or similar properties. A variety of simulation parameters, such as cutoffs, long-range Lennard-Jones corrections, and other factors can impact computed properties. | |
| + | '''Additional work needed.''' | ||
| − | == | + | == Cycle closure in relative free energy calculations == |
| − | = | + | == Further replica-exchange convergence diagnostics == |
| − | = | + | === Round-trip times to determine poorly mixing sets of thermodynamic states === |
| − | + | Even though exchange rates among neighboring states may appear high, or the observed state-to-state transition matrix may appear to be rapidly mixing, it is still possible for slow conformational transitions to trap the replica in a region of conformation space that also traps in a limited subset of thermodynamic states. The following example illustrates three replicas in a Hamiltonian exchange simulation being trapped in this way: | |
| + | : [[File:replica-round-trips.png]] | ||
| + | One way to determine whether this is occurring is to compute the number of ''replica round trips'' in the equilibrated region of a simulation, or to compute the ''average replica round trip time''. This is commonly used as a diagnostic of convergence rates in demonstrating relative efficiencies of different replica exchange schemes: e.g. [http://dx.doi.org/10.1002/jcc.23113 doi] | ||
| − | = | + | = Examples = |
| − | == | + | == Hamiltonian exchange simulation using MBAR == |
| − | + | An illustrative example of computing some of these checks for a Hamiltonian exchange alchemical free energy calculation is [http://nbviewer.ipython.org/urls/gist.github.com/jchodera/139dc026272093c52f68/raw/96c52c7a57bf345bb9c73fd96560ac8e4b0d25d4/YANK+analysis+example.ipynb?create=1 available here]. | |
| − | + | '''JDC: Clean this up and show a simplified "post-simulation health report" report format.''' | |
| − | + | Recommended health check: | |
| + | * Monitor replica exchange state transition probabilities to ensure good alchemical state spacing and replica exchange convergence. | ||
| + | * Automatically determine equilibrated region, and ensure this hasn't discarded most of the simulation data. | ||
| + | * Compute number of effectively uncorrelated samples in equilibrated region, and check <math>N_{eff} > 20</math>. | ||
| + | * Check MBAR overlap matrix dominant eigenvalue gap to ensure good overlap. | ||
| + | * Compute free energy differences and statistical uncertainties for both individual replicas and whole-simulation to check concordance. | ||
| + | * Check replica round-trip numbers and times to ensure no replica trapping is occurring | ||
| + | * In case of poor convergence, search for degrees of freedom coupled with <math>\partial U / \partial \lambda</math> or <math>\Delta u_{ij}(x) \equiv u_j(x) - u_i(x)</math>. | ||
Latest revision as of 01:41, 14 February 2014
Purpose
This page contains a discussion regarding a draft standard practice for analyses to be run following an alchemical free energy calculation to provide a "health report" indicating the quality of an alchemical free energy calculations, and identifying some common modes of failure generally known to occur in these types of calculations. The hope is to begin a community discussion on this topic so that multiple implementations of these standard checks will be available for different popular codes.
Standard steps for post-simulation analysis
Division of simulation data into "equilibrated region" and "production analysis region"
While a Markov chain Monte Carlo simulation does not require that any initial "equilibration" region be identified and discarded to achieve asymptotically consistent results (see Charles Geyer's discussion Burn-In is Unnecessary), the initial starting configuration and box volumes for an alchemically free energy calculation are often so highly atypically samples from the equilibrium distribution that failing to discard some initial transients of relaxation to equilibrium will lead to highly biased free energy estimates. It is therefore recommended that all simulations properly identify a division between the initial "unequilibrated region", in which the system transiently relaxes to a more typical set of samples from equilibrium, and the "equilibrated production region" of data that is analyzed to produce estimates of the free energy. This also allows the analyst to ensure that the "equilibrated region" is sufficiently long as to produce a useful estimate to the practitioner.
This should be done for each "leg" of the alchemical free energy simulation thermodynamic cycle.
Manual inspection of key properties
If properties of the simulation are to be inspected manually (which is not recommended, but may be useful for graphical illustration), the practitioner is advised to examine the following properties:
Box volume
Many simulation preparation schemes for explicit solvent simulations utilize a scheme that replicates a small equilibrated water box (potentially generated with a different solvent or a different set of nonbonded simulation cutoffs or dispersion corrections), places the complex or ligand within this box, and then culls waters with significant overlap with the solute molecules. Counterions are added through one of several heuristic schemes. This process can lead to initial solvent densities that significantly different densities than the average equilibrium density, where density deviations of even 0.1% are highly significant and can result in enormous artificial pressure deviations.
Additionally, initiating a simulation containing an alchemically-modified solute from configurations typical of an unmodified solute will have incorrect initial solvent densities.
We recommend some quantity relating to the box volume be computed and examined over the course of the simulation, examining this for transients
Individual alchemical simulations can be inspected separately.
Replica-exchange simulations are more difficult to inspect because exchanges between replicas complicate the inspection of per-state traces, while per-replica traces hop among many alchemical states with different typical volumes. Therefore, it is recommended that the average volume across all replicas be inspected as a function of simulation time to inspect for initial transients.
TODO: Show examples
Hydrogen bonding
Hydrogen bonds within a system often equilibrate substantially more slowly than other properties. For example, hydrogen bonding between a ligand and binding-site water, between a receptor and surrounding water, and perhaps sometimes even between the ligand and receptor itself, can be slow to reach their equilibrium values. In many cases, timescales for this equilibration in the number of hydrogen bonds to water, for example, can be substantially slower than timescales for apparent equilibration of the system potential energy, for example.
Reduced potential
For a standard simulation sampling from a single thermodynamic state, the reduced potential is given by
- [math]\displaystyle{ u(x_t) = - \ln \pi(x_t) + c }[/math]
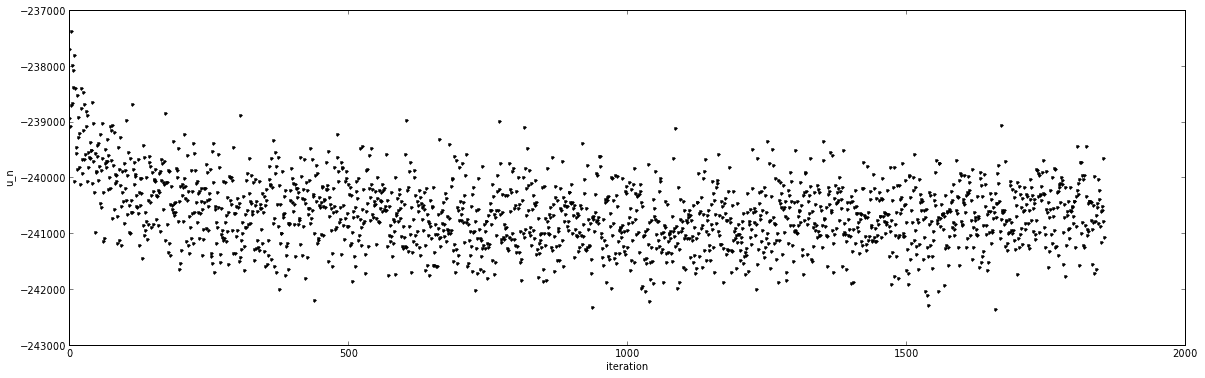
where [math]\displaystyle{ \pi(x) }[/math] represents the normalized probability density for the MCMC simulation, [math]\displaystyle{ x_t }[/math] is the sampled simulation state of the system at time index [math]\displaystyle{ t }[/math] (which may include positions, velocities, box vectors, etc.), and [math]\displaystyle{ c }[/math] is an arbitrary additive constant.
For example, if independent simulations of Hamiltonians [math]\displaystyle{ H_k }[/math] are carried out for [math]\displaystyle{ k = 1,\ldots,K }[/math], simulation index [math]\displaystyle{ k }[/math] would use the quantity
- [math]\displaystyle{ u_k(x_t) = \beta_k H_k(x) }[/math]
where [math]\displaystyle{ \beta_k = (k_B T_k)^{-1} }[/math] is the inverse temperature of simulation index [math]\displaystyle{ k }[/math].
For Hamiltonian exchange (replica-exchange among Hamiltonians) simulations, the appropriate quantity is
- [math]\displaystyle{ u(X_t) = \sum_{k=1}^K u_{s_k}(x_{kt}) = \sum_{k=1}^K \beta_{s_{kt}} H_{s_{kt}}(x_{kt}) }[/math]
where [math]\displaystyle{ X_t = \{x_{1t}, \ldots, x_{Kt}\} }[/math] denotes the set of sampled simulation states at simulation iteration or time index [math]\displaystyle{ t }[/math], and [math]\displaystyle{ s_{kt} }[/math] is the thermodynamic state index sampled by replica [math]\displaystyle{ k }[/math] at simulation iteration or time index [math]\displaystyle{ t }[/math].
This quantity looks like this for a typical Hamiltonian exchange alchemical free energy calculation:
Automated equilibration determination
It is highly recommended that an automated method instead be employed for dividing the simulation history into "unequilibrated" and "equilibrated" regions, though manual inspection of the properties suggested to verify the automated scheme has correctly divided the simulation is often a good visual check of simulation quality.
One concept useful in developing automated equilibration detection points is the notion that the simulation should rapidly sample many uncorrelated samples after reaction the "typical, equilibrated" region of configuration space. This allows us to formulate a scheme such as the following:
It is recommended that the production region of the simulation trajectory be defined as the interval that terminates at the end of the simulation and begins at the time which maximizes the number of uncorrelated samples in that interval. This scheme is a simpler form of one suggested by Wei Yang that requires statistical assumptions of normality. To implement such a scheme, several equally-spaced origins [math]\displaystyle{ t_0 }[/math] of the simulation interval are considered, and the number of uncorrelated configurations in the intervals [math]\displaystyle{ [t_0, T] }[/math] are computed, where [math]\displaystyle{ T }[/math] denotes the end of the simulation. (DLM: We have found that in some cases this seems to lead us astray; I've asked P. Klimovich who did this work to comment on this with details.)
For each interval, the number of effectively uncorrelated configurations [math]\displaystyle{ N_{eff} }[/math] is given by: [math]\displaystyle{ N_{eff} = (T - t_0 + 1) / g }[/math]
where [math]\displaystyle{ g = 1 + 2 \tau }[/math] is the statistical inefficiency computed for the interval [math]\displaystyle{ [t_0, T] }[/math], with [math]\displaystyle{ \tau }[/math] denoting the integrated autocorrelation time computed over that interval.
An example of this for a Hamiltonian-exchange simulation can be seen here:
The maximum of [math]\displaystyle{ N_{eff} }[/math] represents the best choice of [math]\displaystyle{ t_0 }[/math], the beginning of the production region.
Note that a robust scheme for estimating the integrated autocorrelation time / statistical inefficiency must be used, and these results will depend somewhat on that choice in tricky examples. The pymbar package contains a timeseries module that may be useful for this purpose. A robust scheme is described in Sections 2.4 and 5.2 of this JCTC paper, though FFT-based methods can be much faster.
The statistical inefficiency [math]\displaystyle{ g }[/math] should be computed for an appropriate property of the simulation. If there are structural relaxation times known to be critical, these should be evaluated and the maximum statistical inefficiency over these considered as the effective statistical inefficiency of note.
If obvious structural relaxation times are not available, the appropriate time-dependent quantity to use for computation of the statistical inefficiency [math]\displaystyle{ g }[/math] is the reduced potential---the negative logarithm of the unnormalized probability density. But note that in practice, apparent correlation times in the reduced potential may be much lower, especially in explicit solvent, due to the fraction of the system consisting of solvent. Hence, it is especially important to use the maximum relaxation time among important observables. (MRS: In that case, what about the total energy - (water-water) energy? Not always available, but does avoid the problem you mention. Another quantity is dH/dlambda)
While only a rule of thumb, we suggest the equilibrated production region contain at least 20 statistically uncorrelated samples per thermodynamic state. If fewer samples are obtained, the statistical error estimate of methods like BAR and MBAR will be unreliable.
Verifying acceptable alchemical state overlap
It is critical that the alchemical states (or, more generally, thermodynamic states) simulated have sufficient phase space overlap to connect the two endstates of interest. Poor overlap is the reason many simulations fail, introducing large biases or errors into the computed results. Data analysis techniques like TI, BAR, or MBAR may not clearly indicate that phase space overlap is poor without additional computation (though slow convergence of MBAR is often a sign of poor overlap, as is inconsistency between analysis techniques such as TI, BAR, and MBAR).
We recommend that explicit steps be taken to ensure good phase space overlap between all simulated thermodynamic states.
Several approaches can be used to verify this.
Computation of the overlap matrix in MBAR
Those using MBAR to analyze simulations can utilize the calculation of the overlap matrix among alchemical states to verify whether there is sufficient overlap among states to ensure the graph of states is well-connected.
The overlap matrix [math]\displaystyle{ {\bf O} \equiv (o_{ij}) }[/math] is defined by its elements
- [math]\displaystyle{ o_{ij} \equiv \int dx \frac{\pi_i(x) \pi_j(x)}{\sum\limits_{k=1}^K (N_k/N) \pi_k(x)} }[/math]
where [math]\displaystyle{ \pi_i(x) }[/math] is the probability density function for alchemical state [math]\displaystyle{ i }[/math], [math]\displaystyle{ N_k }[/math] is the number of samples collected from state [math]\displaystyle{ k }[/math], and [math]\displaystyle{ N \equiv \sum_{k=1}^K N_k }[/math] is the total number of samples collected.
The larger the gap between the first and second largest eigenvalues of [math]\displaystyle{ {\bf O} }[/math], the better connected all states are. A small gap or degenerate dominant eigenvalues indicates the states are poorly connected.
Michael Shirts: Can you fill in more about this issue? The [math]\displaystyle{ i }[/math]th row of the [math]\displaystyle{ {\bf O} }[/math] matrix described the normalized probability of a given sample from the [math]\displaystyle{ i }[/math]th to have been generated in the [math]\displaystyle{ j }[/math]th state. For example, if all entries are equal, then the average sample from the [math]\displaystyle{ i }[/math]th state is equally likely to have been generated in all states, indicative of very high overlap. If only the diagonal element is populated, then it means that there is essentially no chance that sample could have come from any other state than the [math]\displaystyle{ i }[/math]th state, which is obviously very poor overlap.
(DLM: Also, we found that in some cases, picking a time to consider as "equilibrated" which minimizes g actually results in poorer overlap among states. MRS: does this comment belong here, or in a different section.)
Pairwise computation of overlap with BAR
In a similar manner to MBAR above, elements of the overlap matrix [math]\displaystyle{ {\bf O} \equiv (o_{ij}) }[/math] can be computed among those pairs of states for which data is available for a BAR computation is possible. The overlap matrix will be sparse, but its dominant eigenvalue gap can still be analyzed in a manner identical to that above with MBAR.
(MRS: better to go directly to Bennett's paper, which which he shows there is a direct connection between the estimated uncertainty of the calculation and the overlap. So whether the overlap is enough is pretty much the same as asking whether the statistical uncertainty is low enough.)
Replica-exchange acceptance probabilities
In a standard replica-exchange simulation, exchanges are generally attempted only between pairs of replicas that are "neighbors" in some thermodynamically topological sense. (Note that recent work has shown there are more efficient ways to conduct exchanges.)
In these simulations, examining the fraction of exchange attempts between neighbors that result in acceptance is a good way to tell if overlap is poor, as poor exchange acceptance probabilities is indicative of poor overlap.
Aside: Poor exchange rates will also indicate the benefit of replica exchange is not fully realized because of kinetic bottlenecks in the move through thermodynamic state space, hindering convergence. Note that good neighbor exchange rates can be deceptive---it is only a necessary, but not sufficient, condition for convergence. There are numerous cases where replicas still poorly mix globally even though it appears that all pairs of thermodynamic states have high exchange probabilities. These issues are best diagnosed by looking at round-trip times between the two extreme states of interest. Later sections cover this issue in more detai.
Replica-exchange mixing statistics
If a replica exchange simulation is performed using the recently-proposed Gibbs sampling state mixing scheme, exchanges are attempted between replicas that are not simply "neighbors". This allows the construction of an empirical state-to-state transition matrix [math]\displaystyle{ T_{ij} = P(s_{t+1} = j | s_{t} = i) }[/math], which represents the probability of observing a replica currently in state [math]\displaystyle{ i }[/math] in state [math]\displaystyle{ j }[/math] in the next iteration. This matrix can be constructed for "standard" replica exchange simulations as well, but will be banded tridiagonal.
We can analyze the "mixing statistics" of the equilibrated part of the simulation to ensure that the [math]\displaystyle{ (X,S) }[/math] chain is mixing reasonably well among the various alchemical states. In practice, this is done by recording the number of times a replica transitions from alchemical state i to state j in a single iteration. We can use the fact that the overall chain must obey detailed balance to ensure all eigenvalues of the estimated transition matrix are real.
Note that if the subdominant eigenvalue would have been unity, then the chain would be decomposable, meaning that it completely separated into two separate sets of alchemical states that did not mix. This would have been an indication of poor phase space overlap between some alchemical states. In practice, it's a great idea to monitor these statistics as the simulation is running, even if no data is discarded to equilibration at that point. They give not only a good idea of whether sufficient mixing is occurring, but it provides a lower bound on the mixing time in configuration space. If the configuration x sampling is infinitely fast so that x can be considered to be at equilibrium given the instantaneous permutation S of alchemical state assignments, the subdominant eigenvalue [math]\displaystyle{ \lambda_2 \in [0,1] }[/math] gives an estimate of the mixing time of the overall [math]\displaystyle{ (X,S) }[/math] chain:
- [math]\displaystyle{ \tau_{eq} = \frac{1}{1 - \lambda_2} }[/math]
Computation of statistical error
To Do
(MRS: bootstrap turns out to be very useful. http://pubs.acs.org/doi/abs/10.1021/ct2003995 analyzes a bunch of different methods.)
Some discussion of block bootstrapping.
Determining whether the calculation has converged
Block simulation analysis
A common scheme for diagnosing convergence is to break the simulation into two or more statistically uncorrelated blocks and analyze these blocks independently. Concordance between estimates derived from each block is suggestive that the simulation has run long enough to converge, since each statistically independent subset acts like a statistical sample from the target density.
Care should be taken with this approach, as it is often difficult to decompose the simulation into blocks that are indeed statistically independent. This requires, at minimum, computation of the statistical inefficiency of the simulation to determine how far apart these blocks must be to be statistically uncorrelated.
Even then, it is difficult to ensure that no very long correlation times that are difficult to detect via a statistical inefficiency estimation procedure are in fact present. This test is to be regarded as a necessary, but not sufficient, test for convergence.
If a replica-exchange simulation is used, this test can still be performed, but subsequent sections enumerate more useful tests for convergence.
In general, we believe that block analysis is not nearly a strenuous enough test of convergence, and that analysis of replicate simulations from alternate starting structures is a far better means of accomplishing a similar end, as discussed in the following section.(DLM added this recommendation AGAINST this; is it OK with you?)
Gelman-Rubin convergence criteria for replica-exchange simulations
In 1992, Gelman and Rubin proposed a very clever idea for a convergence diagnostic in the case that multiple MCMC samplers are run from different initial sampler states DOI.
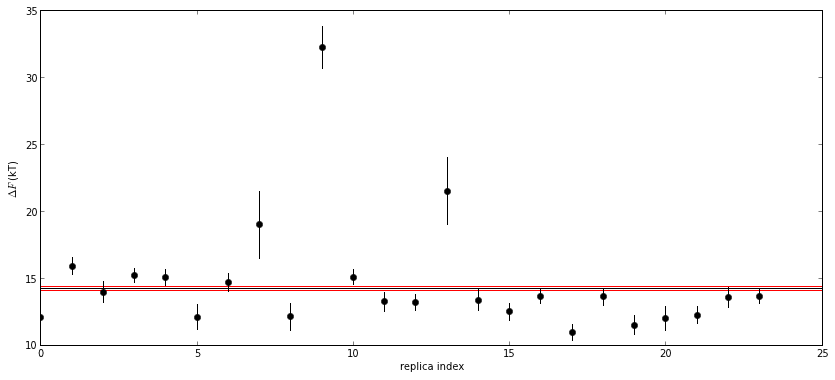
The idea is simple: Each chain gives an individual estimate for some computed expectation or property, and the whole collection of chains give a (presumably more precise) estimate. These chains could be entirely separate sets of free energy calculations run from different starting structures, or different replicas within a replica exchange setup. We can simply compare the individual estimates to the overall estimate to determine whether the chains have been run long enough to see concordance between the individual and global estimates, to within appropriate statistical error. If not, then the samplers have not yet run long enough to sample all of the important modes of the density. Considering the case of replica exchange, we can apply a similar idea, especially if we have initialized our replicas with different configurations (e.g. different docked ligand conformations, and potentially different protein conformations as well). Let's first compute the global estimate of the free energy differences between thermodynamic states using all replicas: (MRS: how do you calculate the free energy differences between state using only single replicas? I'm sure what "global" and "local" free energy differences are in this context. Confusing example)
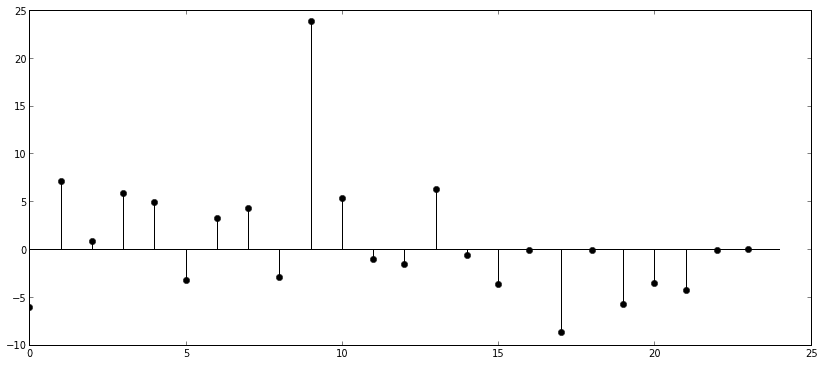
The global and replica estimates are shown with two standard errors (approximate 95% confidence intervals). If the simulation has converged, each nearly independent replica estimate should have a 5% of the replicas should be outside this interval. We can turn these deviations into Z-scores:
This could be used to formulate a statistical test for convergence.
We propose that replicas be initiated with different initial conformations (such as different ligand poses and/or protein models) and a Gelman-Rubin analysis performed to assess convergence.
Comparison of multiple independent simulations
Detection of infrequent events coupled to the alchemical free energy
Often, slow degrees of freedom can couple strongly to the quantities relevant to the estimation of the alchemical free energy difference (such as [math]\displaystyle{ \partial u/\partial \lambda }[/math] in TI or [math]\displaystyle{ \Delta u_{ij} \equiv u_j - u_i }[/math] in BAR/MBAR). We hope that this manifests itself in strong components of the correlation function integrated to estimate the statistical inefficiency, but this may not always happen. Instead, we can examine the simulation for degrees of freedom strongly coupled to these terms.
Here is an example of the slow torsional transitions of the sidechain of Val111, a residue lining the cavity binding site of T4 lysozyme L99A while binding to p-xylene:
(MRS: wouldn't the best way to find DoF coupled to TI would be to look at dh/dl? What does du/dl look like for these trajectories? Is that one step towards the automated approach?)
A more automated approach to detect these types of events is to examine the number of transitions for important structural features and ensure this is sufficient. For example, one can automatically count torsional transitions for sidechains around a ligand binding site, or torsions within a ligand. Whenever timescales are fast compared to the simulation time, or transition counts are high, it is reassuring. And whenever the number of transitions is zero, it may be because alternate conformations are extremely unfavorable. But, whenever transition counts are low but non-negligible (i.e. when timescales are long) it is a warning sign that further investigation may be needed.
Detection of artifacts in the simulation parameters
It is important to regularly validate your employed setup against standard results in test systems with known results, such as hydration free energies, and ideally binding free energies or similar properties. A variety of simulation parameters, such as cutoffs, long-range Lennard-Jones corrections, and other factors can impact computed properties.
Additional work needed.
Cycle closure in relative free energy calculations
Further replica-exchange convergence diagnostics
Round-trip times to determine poorly mixing sets of thermodynamic states
Even though exchange rates among neighboring states may appear high, or the observed state-to-state transition matrix may appear to be rapidly mixing, it is still possible for slow conformational transitions to trap the replica in a region of conformation space that also traps in a limited subset of thermodynamic states. The following example illustrates three replicas in a Hamiltonian exchange simulation being trapped in this way:
One way to determine whether this is occurring is to compute the number of replica round trips in the equilibrated region of a simulation, or to compute the average replica round trip time. This is commonly used as a diagnostic of convergence rates in demonstrating relative efficiencies of different replica exchange schemes: e.g. doi
Examples
Hamiltonian exchange simulation using MBAR
An illustrative example of computing some of these checks for a Hamiltonian exchange alchemical free energy calculation is available here.
JDC: Clean this up and show a simplified "post-simulation health report" report format.
Recommended health check:
- Monitor replica exchange state transition probabilities to ensure good alchemical state spacing and replica exchange convergence.
- Automatically determine equilibrated region, and ensure this hasn't discarded most of the simulation data.
- Compute number of effectively uncorrelated samples in equilibrated region, and check [math]\displaystyle{ N_{eff} \gt 20 }[/math].
- Check MBAR overlap matrix dominant eigenvalue gap to ensure good overlap.
- Compute free energy differences and statistical uncertainties for both individual replicas and whole-simulation to check concordance.
- Check replica round-trip numbers and times to ensure no replica trapping is occurring
- In case of poor convergence, search for degrees of freedom coupled with [math]\displaystyle{ \partial U / \partial \lambda }[/math] or [math]\displaystyle{ \Delta u_{ij}(x) \equiv u_j(x) - u_i(x) }[/math].