Constructing a Pathway of Intermediate States

Free Energy Fundamentals
Theory Definitions Exponential Averaging / Zwanzig Thermodynamic Integration Bennett Acceptance Ratio WHAM MBAR
Methods of Free Energy Simulations Thermodynamic Cycle Intermediate States (Constructing) Soft Core Potentials Running Simulations Extracting Simulation Information Analysis / Bootstrap Sampling
Improving Sampling and Accelerating Simulations Umbrella Sampling Hamiltonian Replica Exchange [math]\displaystyle{ \lambda }[/math]-dynamics / Expanded Ensemble

Free Energy How-to's
Example Calculations Absolute Solvation Free Energy Relative Binding Affinity Absolute Binding Affinity
Tutorials Ethanol Solvation - GROMACS Expanded Ensemble - GROMACS Absolute Binding Free Energy - GROMACS

Because the phase space between two target states of interest can be near zero, doing free energy calculations for the two states alone will often have very large errors. When one considers the large number of potential molecules that could be considered interesting, this problem becomes even more pronounced. Because free energy is a state function, we can construct a thermodynamic path that takes us through a set of states that improves phase space overlap between states. To put this mathematically, we can improve our results by constructing high phase space overlap intermediates and calculating our free energy difference by

[math]\displaystyle{ \Delta A_{1,K} = \sum_{i=1}^{K-1} \Delta A_{i,i+1} }[/math].

One advantage available to computational free energy calculations is the ability to simulate unphysical states. By this, we mean that our intermediate states do not have to be observable experimentally. This is a fact that most if not all computational methods out there take advantage of. Again, because free energy is a state function, we simply choose the path of greatest convenience and carry out the calculation across this path. However, choosing the "correct" or even a "good" path is a very challenging action and is one of the most difficult tasks in the entire field of free energy calculations.

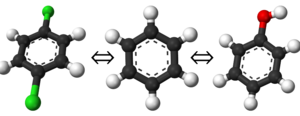
Because our free energy calculations frequently involve transforming one kind of atom at a given site to another kind, the transformations are often referred to as "alchemical."

Linear Alchemical Potential

To be more clear about what it means to define an "alchemical path," one should think of it as defining the thermodynamic path where we modify, remove, or add various forces on an atom. Take for instance estimating the free energy difference between a Lennard-Jones fluid and a Stockmayer fluid, our thermodynamic path would calculate the work and free energy required to switch on the dipole interactions at a rate that maximizes phase space overlap and efficiency. Because the atoms changed their interactions with the surroundings without being removed or added from the system, we have directly modified the atoms to create our alchemical path.

Most alchemical transformations can be defined by alchemically scaling the potential in some manner. The simplest of these is the linear transformation, which says that the net potential energy, [math]\displaystyle{ U(\lambda,\vec{q}) }[/math], is the sum of the alchemically modified two end states' potentials, [math]\displaystyle{ U_0 }[/math] and [math]\displaystyle{ U_1 }[/math], plus the parts of the potential that are unaffected by the alchemical transformation, [math]\displaystyle{ U_{unaffected} }[/math]; or

[math]\displaystyle{ U(\lambda,\vec{q}) = (1-\lambda) U_0(\vec{q}) + \lambda U_1(\vec{q}) + U_{\mathrm{unaffected}}(\vec{q}) }[/math]

where the alchemical variable linearly modifies the confrontational information from each state of interest.

Soft Core Potentials

Placeholder!!!!