Constructing a Pathway of Intermediate States
| Free Energy Fundamentals |
|---|
 |
|
Methods of Free Energy Simulations
|
| Free Energy How-to's |
|---|
 |
Because the phase space between two target states of interest can be near zero, doing free energy calculations for the two states alone will often have very large errors. When one considers the large number of potential molecules that could be considered interesting, this problem becomes even more pronounced. Because free energy is a state function, we can construct a thermodynamic path that takes us through a set of states that improves phase space overlap between states. To put this mathematically, we can improve our results by constructing high phase space overlap intermediates and calculating our free energy difference by
- [math]\displaystyle{ \Delta A_{1,K} = \sum_{i=1}^{K-1} \Delta A_{i,i+1} }[/math].
One advantage available to computational free energy calculations is the ability to simulate unphysical states. By this, we mean that our intermediate states do not have to be observable experimentally. This is a fact that most if not all computational methods out there take advantage of. Again, because free energy is a state function, we simply choose the path of greatest convenience and carry out the calculation across this path. However, choosing the "correct" or even a "good" path is a very challenging action and is one of the most difficult tasks in the entire field of free energy calculations.
Because our free energy calculations frequently involve transforming one kind of atom at a given site to another kind, the transformations are often referred to as "alchemical."
Linear Alchemical Potential
To be more clear about what it means to define an "alchemical path," one should think of it as defining the thermodynamic path where we modify, remove, or add various forces on an atom. Take for instance estimating the free energy difference between a Lennard-Jones fluid and a Stockmayer fluid, our thermodynamic path would calculate the work and free energy required to switch on the dipole interactions at a rate that maximizes phase space overlap and efficiency.[1] Because the atoms changed their interactions with the surroundings without being removed or added from the system, we have directly modified the atoms to create our alchemical path.
Most alchemical transformations can be defined by alchemically scaling the potential in some manner. The simplest of these is the linear transformation, which says that the net potential energy, [math]\displaystyle{ U(\lambda,\vec{q}) }[/math], is the sum of the alchemically modified two end states' potentials, [math]\displaystyle{ U_0 }[/math] and [math]\displaystyle{ U_1 }[/math], plus the parts of the potential that are unaffected by the alchemical transformation, [math]\displaystyle{ U_{unaffected} }[/math]; or
- [math]\displaystyle{ U(\lambda,\vec{q}) = (1-\lambda) U_0(\vec{q}) + \lambda U_1(\vec{q}) + U_{\mathrm{unaffected}}(\vec{q}) }[/math]
where the alchemical variable linearly modifies the confrontational information from each state of interest.
Problems with Linear Transformations
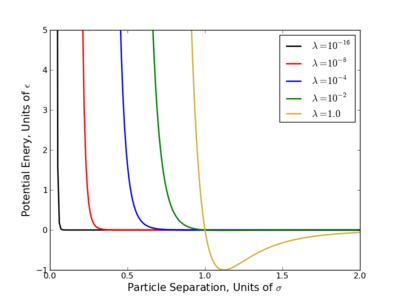
The largest problem with linear scaling is that it does not provide equal phase space overlap between states. This has been a long acknowledged problem with several easy to see reasons why.
- Consider the OPLS-AA force field, at [math]\displaystyle{ \lambda=0.1 }[/math], the excluded volume of a methane sphere is still 60-70%.
- Most potential energy functions have an infinite potential (singularity) at [math]\displaystyle{ r=0 }[/math]. This is usually brought on by the [math]\displaystyle{ r^{-12} }[/math] term that appears in Lennard-Jones based potentials and is present at all nonzero values of [math]\displaystyle{ \lambda }[/math]. Since most the free energy techniques require some numeric methods, evaluating this singularity diverges the calculations.
This singularity causes the most problems with TI since that method requires evaluation [math]\displaystyle{ \frac{dU}{d\lambda} }[/math] numerically, which diverges at the singularity. Several workaround for this have been suggested where one of the simplest is do raise the [math]\displaystyle{ \lambda }[/math] terms to a power greater than or equal to 4 like so
- [math]\displaystyle{ \displaystyle U(\lambda) = (1-\lambda)^4 U_0 + \lambda^4 U_1 }[/math]
These methods do converge [math]\displaystyle{ \left\langle\frac{dU}{d\lambda} \right\rangle }[/math] however very slowly with number of samples and still can cause numeric instabilities[3][4]
Other methods have been suggested such as shrinking the core of the tom, but this also causes instabilities[3][5][6] and are not practical for systems with many bonds.
Soft Core Potentials
A standard method has been developed to alchemically change molecules to get around the numeric instabilities called a "soft core potential."[2][7] In these potentials, the configuration variable, [math]\displaystyle{ r }[/math], is now coupled to the alchemical variable, [math]\displaystyle{ \lambda }[/math], smoothing out the singularity and looks like
- [math]\displaystyle{ U(\lambda,r) = 4\epsilon\lambda^n \left[\left(\alpha(1-\lambda)^m + \left(\frac{r}{\sigma}\right)^6\right)^{-2} + \left(\alpha(1-\lambda)^m + \left(\frac{r}{\sigma}\right)^6\right)^{-1}\right] }[/math]
where [math]\displaystyle{ \alpha }[/math] is a constant (usually 0.5) and, [math]\displaystyle{ m }[/math] and [math]\displaystyle{ n }[/math] are positive integers with the original choice being [math]\displaystyle{ n=4 }[/math] and [math]\displaystyle{ m=2 }[/math]. Recent improvements have shown that keeping [math]\displaystyle{ \alpha=0.5 }[/math] and setting [math]\displaystyle{ m=n=1 }[/math] provides significant improvement to the variance[3][4][8] and research into further improving this is still going on.[9]
This potential is now considered the "standard" which many software packages now base their free energies on.
Rules of Thumb for Intermediate States
This section is just for the short version of the discussions found elsewhere(mostly below) on the site. These rules are not the end-all set and you should be familiar with why each one is suggested before just accepting them.
- Bonded terms can be modified/turned off linearly. This includes angle or bond force constants as well as unconstrained bond distances.
Constructing Intermediate States
This section outlines some of the options one has when constructing their thermodynamic path through the intermediary states. Each method has its own strengths and weakness and should be carefully considered before implementing. Although there is no absolute best way to do this, there are a number of best practices we strongly consider following, especially for those starting out in free energy calculations.
References
- ↑ Frenkel, D., & Smit, B. (2002). Understanding Molecular Simulation (2nd ed., p. 638). San Diego: Academic Press.
- ↑ 2.0 2.1 Beutler, T., Mark, A., & Schaik, R. van. (1994). Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chemical Physics Letters, 222(June), 529–539.
- ↑ 3.0 3.1 3.2 Pitera, J. W., and van Gunsteren, W. F. (2002) A comparison of non-bonded scaling approaches for free energy calculations. Mol. Simulat. 28, 45–65.
- ↑ 4.0 4.1 Steinbrecher, T., Mobley, D. L., and Case, D. A. (2007) Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J. Chem. Phys. 127, 214108.
- ↑ Pearlman, D. A., and Connelly, P. R. (1995) Determination of the differential effects of hydrogen bonding and water release on the binding of FK506 to native and TYR82 → PHE82 FKBP-12 proteins using free energy simulations. J. Mol. Biol. 248, 696–717.
- ↑ Wang, L., and Hermans, J. (1994) Change of bond length in free-energy simulations: Algorithmic improvements, but when is it necessary? J. Chem. Phys. 100, 9129–9139.
- ↑ Zacharias, M., Straatsma, T. P., and McCammon, J. A. (1994) Separation-shifted scaling, a new scaling method for Lennard-Jones interactions in thermodynamic integration. J. Phys. Chem. 100, 9025–9031.
- ↑ Shirts, M. R., and Pande, V. S. (2005) Solvation free energies of amino acid side chains for common molecular mechanics water models. J. Chem. Phys. 122, 134508.
- ↑ Pham, T. T., and Shirts, M. R. (2011) Identifying Low Variance Pathways for Free Energy Calculations of Molecular Transformations in Solution Phase. J. Chem. Phys. 135, 034114.