Example: Relative Binding Affinity
| Free Energy Fundamentals |
|---|
 |
|
Methods of Free Energy Simulations
|
| Free Energy How-to's |
|---|
 |
This example will be a bit more complex than the solvation example since we are now transforming one molecule to another within an environment. Again, the purpose of this page is not to take you through step-by-step the process of simulation, but instead guide you through the logical decisions that can be applied to any simulation package of your choosing. We will work through the same questions that were asked on the previous example as these should be asked for any free energy simulation.
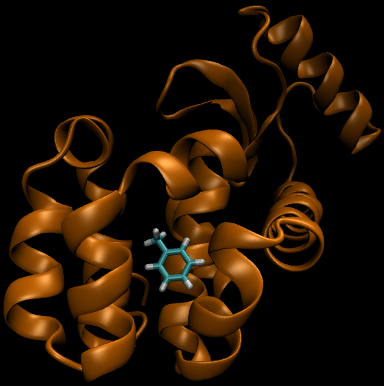
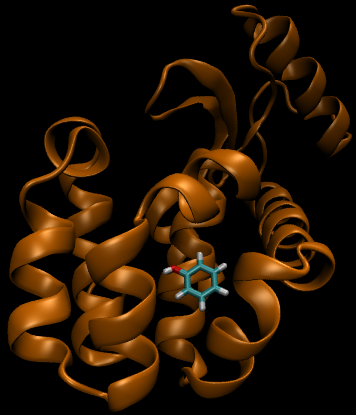
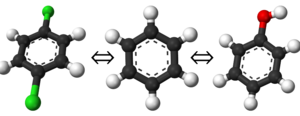
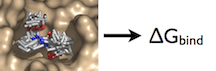
For this particular example, we will look at the difference in the relative binding free energies of toluene and phenol in the apolar cavity of T4 Lysozyme.

|
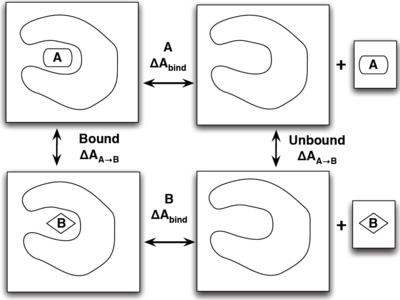
What is the Thermodynamic Cycle?
If you have already read through the thermodynamic cycle page, then you will have already seen this picture on the left. For our simulation, we can define the thermodynamic cycle either by directly converting toluene to phenol (which would be very costly due to the large number of changing interactions and box size), or we can recognize that free energy is a state function and we can use this relation to solve for it as well:
- [math]\displaystyle{ \Delta \Delta A_{\mathrm{bind}} = \Delta A_{\mathrm{bind}}^B - \Delta A_{\mathrm{bind}}^A = \Delta A_{A\rightarrow B}^{\mathrm{bound}} - \Delta A_{A\rightarrow B}^{\mathrm{unbound}} }[/math]
which does not require an excessively large box and can be done relatively simply by choosing the correct intermediate states to transform the ligands.
To provide the visuals for this particular system, please see the rendered images below; note that the solvent can be either implicit or explicit and the cycle will still be valid.
| Abound | left/right arrow +text | Protein | + | A unbound |
| Up down arrow + text | BLANK | Updown arow + text | BLANK | BLANK |
| Bbound | left/right arrow | Protein | + | B unbound |