Draft Standards for Post-Calculation Health Reports

Purpose

This page contains a discussion regarding a draft standard practice for analyses to be run following an alchemical free energy calculation to provide a "health report" indicating the quality of an alchemical free energy calculations, and identifying some common modes of failure generally known to occur in these types of calculations. The hope is to begin a community discussion on this topic so that multiple implementations of these standard checks will be available for different popular codes.

Standard steps for post-simulation analysis

Division of simulation data into "equilibrated region" and "production analysis region"

While a Markov chain Monte Carlo simulation does not require that any initial "equilibration" region be identified and discarded to achieve asymptotically consistent results (see Charles Geyer's discussion Burn-In is Unnecessary), the initial starting configuration and box volumes for an alchemically free energy calculation are often so highly atypically samples from the equilibrium distribution that failing to discard some initial transients of relaxation to equilibrium will lead to highly biased free energy estimates. It is therefore recommended that all simulations properly identify a division between the initial "unequilibrated region", in which the system transiently relaxes to a more typical set of samples from equilibrium, and the "equilibrated production region" of data that is analyzed to produce estimates of the free energy. This also allows the analyst to ensure that the "equilibrated region" is sufficiently long as to produce a useful estimate to the practitioner.

This should be done for each "leg" of the alchemical free energy simulation thermodynamic cycle.

Manual inspection of key properties

If properties of the simulation are to be inspected manually (which is not recommended, but may be useful for graphical illustration), the practitioner is advised to examine the following properties:

Box volume

Many simulation preparation schemes for explicit solvent simulations utilize a scheme that replicates a small equilibrated water box (potentially generated with a different solvent or a different set of nonbonded simulation cutoffs or dispersion corrections), places the complex or ligand within this box, and then culls waters with significant overlap with the solute molecules. Counterions are added through one of several heuristic schemes. This process can lead to initial solvent densities that significantly different densities than the average equilibrium density, where density deviations of even 0.1% are highly significant and can result in enormous artificial pressure deviations.

Additionally, initiating a simulation containing an alchemically-modified solute from configurations typical of an unmodified solute will have incorrect initial solvent densities.

We recommend some quantity relating to the box volume be computed and examined over the course of the simulation, examining this for transients

Individual alchemical simulations can be inspected separately.

Replica-exchange simulations are more difficult to inspect because exchanges between replicas complicate the inspection of per-state traces, while per-replica traces hop among many alchemical states with different typical volumes. Therefore, it is recommended that the average volume across all replicas be inspected as a function of simulation time to inspect for initial transients.

TODO: Show examples

Reduced potential

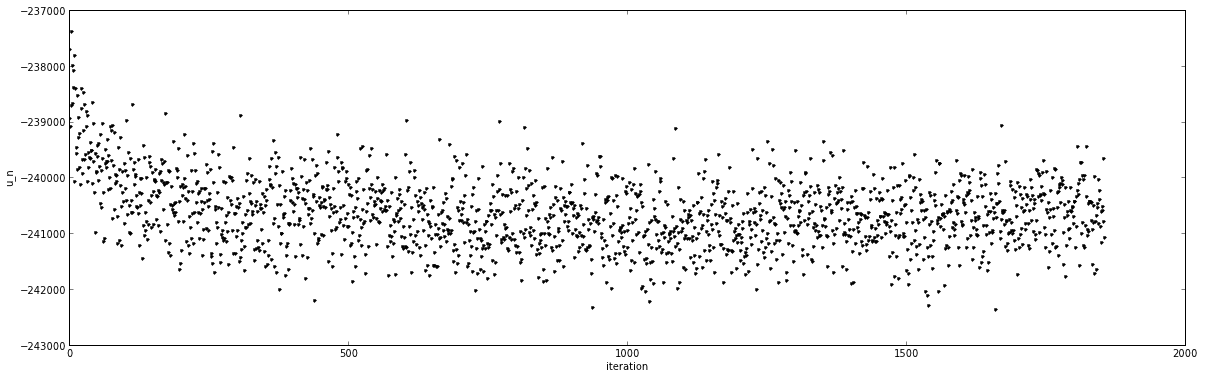
For a standard simulation sampling from a single thermodynamic state, the reduced potential is given by

[math]\displaystyle{ u(x_t) = - \ln \pi(x_t) + c }[/math]

where [math]\displaystyle{ \pi(x) }[/math] represents the normalized probability density for the MCMC simulation, [math]\displaystyle{ x_t }[/math] is the sampled simulation state of the system at time index [math]\displaystyle{ t }[/math] (which may include positions, velocities, box vectors, etc.), and [math]\displaystyle{ c }[/math] is an arbitrary additive constant.

For example, if independent simulations of Hamiltonians [math]\displaystyle{ H_k }[/math] are carried out for [math]\displaystyle{ k = 1,\ldots,K }[/math], simulation index [math]\displaystyle{ k }[/math] would use the quantity

[math]\displaystyle{ u_k(x_t) = \beta_k H_k(x) }[/math]

where [math]\displaystyle{ \beta_k = (k_B T_k)^{-1} }[/math] is the inverse temperature of simulation index [math]\displaystyle{ k }[/math].

For Hamiltonian exchange (replica-exchange among Hamiltonians) simulations, the appropriate quantity is

[math]\displaystyle{ u(X_t) = \sum_{k=1}^K u_{s_k}(x_{kt}) = \sum_{k=1}^K \beta_{s_{kt}} H_{s_{kt}}(x_{kt}) }[/math]

where [math]\displaystyle{ X_t = \{x_{1t}, \ldots, x_{Kt}\} }[/math] denotes the set of sampled simulation states at simulation iteration or time index [math]\displaystyle{ t }[/math], and [math]\displaystyle{ s_{kt} }[/math] is the thermodynamic state index sampled by replica [math]\displaystyle{ k }[/math] at simulation iteration or time index [math]\displaystyle{ t }[/math].

This quantity looks like this for a typical Hamiltonian exchange alchemical free energy calculation:

Automated equilibration determination

It is highly recommended that an automated method instead be employed for dividing the simulation history into "unequilibrated" and "equilibrated" regions, though manual inspection of the properties suggested to verify the automated scheme has correctly divided the simulation is often a good visual check of simulation quality.

One concept useful in developing automated equilibration detection points is the notion that the simulation should rapidly sample many uncorrelated samples after reaction the "typical, equilibrated" region of configuration space. This allows us to formulate a scheme such as the following:

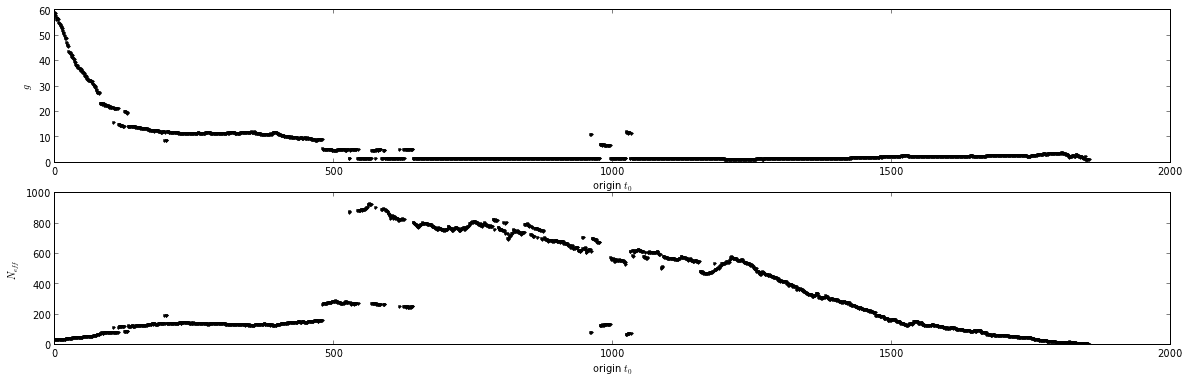
It is recommended that the production region of the simulation trajectory be defined as the interval that terminates at the end of the simulation and begins at the time which maximizes the number of uncorrelated samples in that interval. This scheme is a simpler form of one suggested by Wei Yang that requires statistical assumptions of normality. To implement such a scheme, several equally-spaced origins [math]\displaystyle{ t_0 }[/math] of the simulation interval are considered, and the number of uncorrelated configurations in the intervals [math]\displaystyle{ [t_0, T] }[/math] are computed, where [math]\displaystyle{ T }[/math] denotes the end of the simulation.

For each interval, the number of effectively uncorrelated configurations [math]\displaystyle{ N_{eff} }[/math] is given by

[math]\displaystyle{ N_{eff} = (T - t_0 + 1) / g }[/math]

where [math]\displaystyle{ g = 1 + 2 \tau }[/math] is the statistical inefficiency computed for the interval [math]\displaystyle{ [t_0, T] }[/math], with [math]\displaystyle{ \tau }[/math] denoting the integrated autocorrelation time computed over that interval.

An example of this for a Hamiltonian-exchange simulation can be seen here:

The maximum of [math]\displaystyle{ N_{eff} }[/math] represents the best choice of [math]\displaystyle{ t_0 }[/math], the beginning of the production region.

The integrated autocorrelation time [math]\displaystyle{ g }[/math] should be computed for an appropriate property of the simulation. If there are structural relaxation times known to be critical, these should be evaluated and the maximum statistical inefficiency over these considered as the effective statistical inefficiency of note.

If obvious structural relaxation times are not available, the appropriate time-dependent quantity to use for computation of the statistical inefficiency [math]\displaystyle{ g }[/math] is the reduced potential---the negative logarithm of the unnormalized probability density.

Number of uncorrelated samples

While only a rule of thumb, we suggest the equilibrated production region contain at least 20 statistically uncorrelated samples per thermodynamic state. If fewer samples are obtained, the statistical error estimate of methods like BAR and MBAR will be unreliable.

Verifying acceptable alchemical state overlap

It is critical that the alchemical states (or, more generally, thermodynamic states) simulated have sufficient phase space overlap to connect the two endstates of interest. Poor overlap is the reason many simulations fail, introducing large biases or errors into the computed results. Data analysis techniques like TI, BAR, or MBAR may not clearly indicate that phase space overlap is poor without additional computation (though slow convergence of MBAR is often a sign of poor overlap).

We recommend that explicit steps be taken to ensure good phase space overlap between all simulated thermodynamic states.

Several approaches can be used to verify this.

Computation of the overlap matrix in MBAR

Those using MBAR to analyze simulations can utilize the calculation of the overlap matrix among alchemical states to verify whether there is sufficient overlap among states to ensure the graph of states is well-connected.

The overlap matrix [math]\displaystyle{ {\bf O} \equiv (o_{ij}) }[/math] is defined by its elements

[math]\displaystyle{ o_{ij} \equiv \int dx \frac{\pi_i(x) \pi_j(x)}{\sum\limits_{k=1}^K (N_k/N) \pi_k(x)} }[/math]

where [math]\displaystyle{ \pi_i(x) }[/math] is the probability density function for alchemical state [math]\displaystyle{ i }[/math], [math]\displaystyle{ N_k }[/math] is the number of samples collected from state [math]\displaystyle{ k }[/math], and [math]\displaystyle{ N \equiv \sum_{k=1}^K N_k }[/math] is the total number of samples collected.

The larger the gap between the first and second largest eigenvalues of [math]\displaystyle{ {\bf O} }[/math], the better connected all states are. A small gap or degenerate dominant eigenvalues indicates the states are poorly connected.

Michael Shirts: Can you fill in more about this issue?

Pairwise computation of overlap with BAR

In a similar manner to MBAR above, elements of the overlap matrix [math]\displaystyle{ {\bf O} \equiv (o_{ij}) }[/math] can be computed among those pairs of states for which data is available for a BAR computation is possible. The overlap matrix will be sparse, but its dominant eigenvalue gap can still be analyzed in a manner identical to that above with MBAR.

Replica-exchange acceptance probabilities

In a standard replica-exchange simulation, exchanges are generally attempted only between pairs of replicas that are "neighbors" in some thermodynamically topological sense. (Note that recent work has shown there are more efficient ways to conduct exchanges.)

In these simulations, examining the fraction of exchange attempts between neighbors that result in acceptance is a good way to tell if overlap is poor, as poor exchange acceptance probabilities is indicative of poor overlap.

Aside: Poor exchange rates will also indicate the benefit of replica exchange is not fully realized because of kinetic bottlenecks in the move through thermodynamic state space, hindering convergence. Note that good neighbor exchange rates can be deceptive---it is only a necessary, but not sufficient, condition for convergence. There are numerous cases where replicas still poorly mix globally even though it appears that all pairs of thermodynamic states have high exchange probabilities. These issues are best diagnosed by looking at round-trip times between the two extreme states of interest. Later sections cover this issue in more detai.

Determining whether the calculation has converged

Block simulation analysis

A common scheme for diagnosing convergence is to break the simulation into two or more statistically uncorrelated blocks and analyze these blocks independently. Concordance between estimates derived from each block is suggestive that the simulation has run long enough to converge, since each statistically independent subset acts like a statistical sample from the target density.

Care should be taken with this approach, as it is often difficult to decompose the simulation into blocks that are indeed statistically independent. This requires, at minimum, computation of the statistical inefficiency of the simulation to determine how far apart these blocks must be to be statistically uncorrelated.

Even then, it is difficult to ensure that no very long correlation times that are difficult to detect via a statistical inefficiency estimation procedure are in fact present. This test is to be regarded as a necessary, but not sufficient, test for convergence.

If a replica-exchange simulation is used, this test can still be performed, but subsequent sections enumerate more useful tests for convergence.

Examples

Hamiltonian exchange simulation using MBAR

An illustrative example of computing some of these checks for a Hamiltonian exchange alchemical free energy calculation is available here.

JDC: Clean this up and show a simplified "post-simulation health report" report format.

Recommended health check:

• Monitor replica exchange state transition probabilities to ensure good alchemical state spacing and replica exchange convergence.
• Automatically determine equilibrated region, and ensure this hasn't discarded most of the simulation data.
• Compute number of effectively uncorrelated samples in equilibrated region, and check [math]\displaystyle{ N_{eff} \gt 20 }[/math].
• Check MBAR overlap matrix dominant eigenvalue gap to ensure good overlap.
• Compute free energy differences and statistical uncertainties for both individual replicas and whole-simulation to check concordance.
• Check replica round-trip numbers and times to ensure no replica trapping is occurring
• In case of poor convergence, search for degrees of freedom coupled with [math]\displaystyle{ \partial U / \partial \lambda }[/math] or [math]\displaystyle{ \Delta u_{ij}(x) \equiv u_j(x) - u_i(x) }[/math].