Absolute Binding Free Energy - Gromacs 2016

Free Energy Fundamentals
Theory Definitions Exponential Averaging / Zwanzig Thermodynamic Integration Bennett Acceptance Ratio WHAM MBAR
Methods of Free Energy Simulations Thermodynamic Cycle Intermediate States (Constructing) Soft Core Potentials Running Simulations Extracting Simulation Information Analysis / Bootstrap Sampling
Improving Sampling and Accelerating Simulations Umbrella Sampling Hamiltonian Replica Exchange [math]\displaystyle{ \lambda }[/math]-dynamics / Expanded Ensemble

Free Energy How-to's
Example Calculations Absolute Solvation Free Energy Relative Binding Affinity Absolute Binding Affinity
Tutorials Ethanol Solvation - GROMACS Expanded Ensemble - GROMACS Absolute Binding Free Energy - GROMACS

!!! Page under development !!!

Introduction

In this tutorial we will calculate the free energy of binding (i.e. affinity) of a ligand for a protein using an alchemical pathway. More specifically, in this example based on the published work of Boyce et al. 2009, we will consider the binding of n-phenylglycinonitrile to an engineered T4 lysozyme cavity (L99A/M102Q), starting from an X-ray structure of the protein-ligand complex (PDB-ID 2RBN).

The tutorial assumes knowledge of molecular dynamics (MD) simulations, Gromacs 2016, as well as the basic theoretical aspects of free energy calculations. Before this practical, it is thus suggested to go through >this< ethanol solvation tutorial on alchemistry.org, or >this< methane solvation tutorial written by Justin Lemkul. It is also important to be familiar with ligand-protein simulations, including ligand parameterization. Finally, basic bash and python skills are assumed too, as some of the scripts provided might need to be slightly adapted.

The thermodynamic cycle used to obtain the binding free energy will be reviewed first, and then we will go through the principal steps of the process. The input files needed to run the calculations will be provided, however, you can also set everything up from scratch yourself if you wish (it can be a good exercise, in fact).

For enquiries about the tutorial, and in particular if you find mistakes or have suggestions for improvement, please feel free to email me.

Thermodynamic cycle

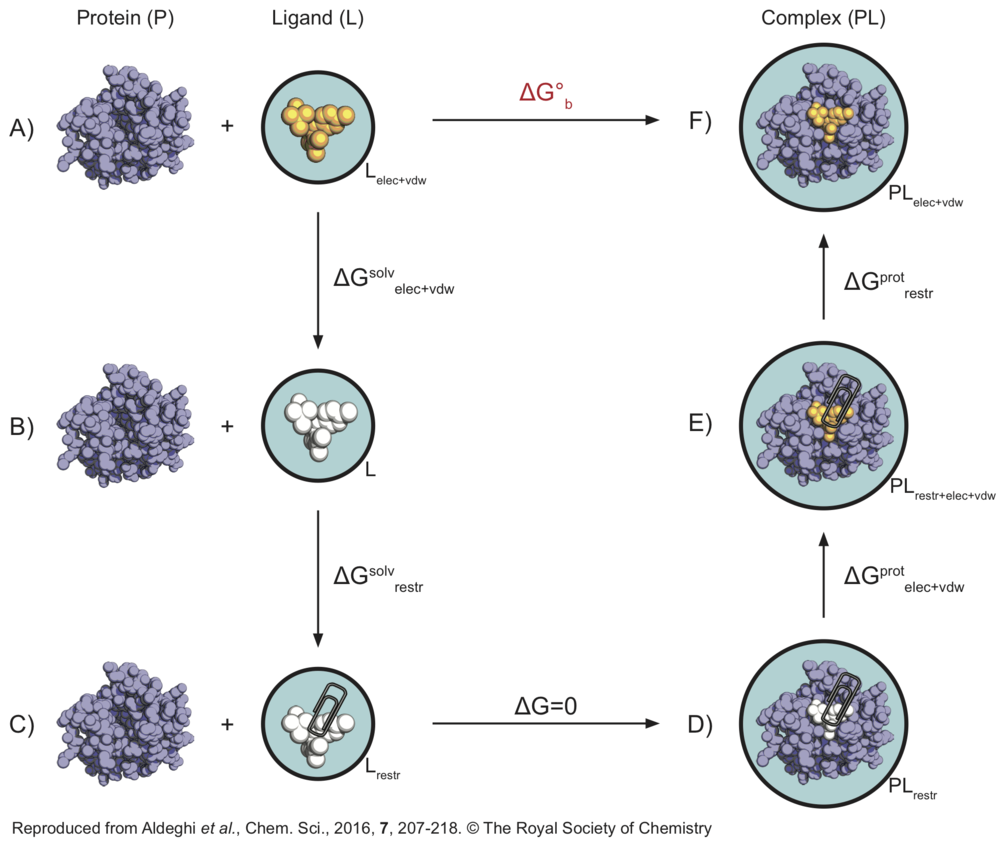
Here is a graphical representation of the cycle we will use in this tutorial, as we find it helpful to visualise the steps needed to carry out the calculations. Its purpose is simply to summarise the steps we will need to consider - if this seems confusing, I would suggest visiting the following pages before proceeding with the tutorial: thermodynamic cycle, absolute binding affinty.

In this thermodynamic cycle, the systems we need to simulate are indicated by a black circle around them, the presence of restraints is indicated by a paperclip, a white ligand means it is not interacting with the environment (i.e. it is decoupled) and the light blue background is a reminder that explicit water is present. The right-hand side leg of the cycle involves simulations of the protein-ligand complex, whereas the left-hand side leg of the cycle involved simulations of the ligand in solution.

What we want to do is to go from to top-left corner of this cycle representing the physical unbound state (state A) to the top-right corner representing the physical bound state (state F), through a series of non-physical (or alchemical) intermediate states (like states B, C, D, and E). From the top-left corner of the cycle (state A), the first step is to decouple the ligand from solution (state B), in order to recover [math]\displaystyle{ \Delta G^{solv}_{elec+vdw} }[/math]. At this point the ligand is not interacting with the environment anymore, so that restraints are introduced in order to keep its position and orientation close to that of the bound pose. The free energy difference [math]\displaystyle{ \Delta G^{solv}_{restr} }[/math] between state B and C will be calculated analytically as described by Boresch et al.. Also note that states C and D are effectively equivalent, since there are no interactions between the ligand (in vacuum) and protein (in solution) systems. Now the ligand's coulombic and vdW interactions are turned on again, and we can compute [math]\displaystyle{ \Delta G^{prot}_{elec+vdw} }[/math]. The ligand is however still restrained, which is not the physical bound state. Therefore, the restraints are finally removed through a series of simulations so that [math]\displaystyle{ \Delta G^{prot}_{restr} }[/math] can be calculated. Once all of the free energy differeces across the alchemical cycle have been calculated, the binding free energy ([math]\displaystyle{ \Delta G^{o}_{b} }[/math]) of the ligand can be recovered.

In this tutorial, we will always calculate the free energy for the decoupling of the ligand (going from top to bottom states of the cycle), since we find helpful to think of the ligand as being in the same state when at lambda=0 (coupled) versus lambda=1 (decoupled). However, this means that in order to sum all free energy terms correctly we will need to invert the sign of [math]\displaystyle{ \Delta G^{prot}_{elec+vdw+restr} }[/math].

Initial setup

In order to have everything ready to run the windows at different lambda values it is necessary to prepare all input files (.gro, .top and .mdp files); the typical Gromacs editconf/solvate/genion steps apply. Briefly, for this exercise the setup is as follows: dodecahedral box with minimum distance of 1.0 nm from the protein, Amber99SB-ILDN force field, TIP3P water model, GAFF parametrization for the ligand with AM1-BCC charges. More details about the parameters are in the .top and .mdp files provided, as well as in the original publication .

You can find the input files needed to complete this tutorial here: Input Files. As it is possible to see from the .mdp files, 20 windows will be used for the ligand in the solution leg of the cycle, and 30 for the protein-ligand complex leg of the cycle. See Note 1 for some comments on the .mdp files.

Ligand decoupling from complex

We will start taking care of the simulations of the complex, as they are more involved. This set of simulations comprises a total of 30 windows, and for each of them energy minimization, NVT and NPT equilibration, and production run (1 ns) are performed.

The set of restraints used is defined by 1 distance, 2 angles and 3 dihedrals harmonic potentials. These restraints have been defined by bonded terms between the ligand and the protein in the topology file (complex.top), using the [ intermolecular_interactions ] section.

In the .mdp files we define 3 lambda vectors: bonded, coulomb, and vdw. In such a way we can use 30 identical .mdp files where we simply choose the state we are simulating with the init-lambda-state variable. As it is possible to see, we first apply the restraints, then we remove the coulombic, and finally the van der Waals interactions. Therefore, by decoupling the ligand, we are going from state F to D according to the thermodynamic cycle above.

We are now ready to run all the simulations and collect all the dhdl.xvg files needed for analysis. The run.sh script provided with the input files can be used to run the energy minimisation, NVT and NPT equilibrations, and production simulation for all lambda windows on your local machine, or it can be adapted to be used on some cluster. See Note 1 for Hamiltonian Replica Exchange.

Once all simulation are completed, it is possible to analyse the results with the alchemical_analysis.py python tool available here. First, it helps to collect all dhdl.xvg files in a folder (e.g. using >this< simple script), then you can analyse all data with the following command:

   alchemical_analysis.py -d 'directory' -p 'prefix' -t 300 -s 100 -u kcal -w -g

This will return the free energy estimate for going from state F to D ([math]\displaystyle{ \Delta G^{prot}_{elec+vdw+restr} }[/math]). To see all the options available, and their meaning, invoke the help by using the -h flag. If you prefer, you can also use the Gromacs tool gmx bar; however, I find alchemical-analysis to be more convenient as it already subsamples the data after calculating the statistical inefficiency, estimates the free energy with various methods (including BAR, MBAR and TI), and prints out results and some useful plots in a tidy format.

For this step of the calculations, with MBAR I obtained:

[math]\displaystyle{ \Delta G^{prot}_{elec+vdw+restr} = 21.192 \pm 0.044 }[/math] kcal/mol

Here is a link to the output I obtained from the alchemical_analysis script: Results for complex. Note that this might not be exactly the number you will get (even if you use exactly the same input files, parameters and Gromacs version I used) but it should be close. In fact, running a total of free complex calculations, with MBAR I obtained a mean and standard deviation of [math]\displaystyle{ 21.181 \pm 0.093 }[/math] kcal/mol.

Ligand decoupling from solution

Now we need to obtain the free energy for the decoupling of the ligand from solution ([math]\displaystyle{ \Delta G^{solv}_{elec+vdw} }[/math]). This set of simulations involve a total of 20 windows. In this case we are only turning off coulombic and Lennard-Jones interactions, since the [math]\displaystyle{ \Delta G^{solv}_{restr} }[/math] can be calculated analytically as later shown.

The results can be obtained again in the same way as we did for the complex, and here is a link to what I obtained after running alchemical_analysis.py: (Results for ligand). MBAR gave me:

[math]\displaystyle{ \Delta G^{solv}_{elec+vdw} = 7.739 \pm 0.021 }[/math] kcal/mol.

Restraints

Adding the restraints to the decoupled ligand (state B to C) can be taken into account analytically using Eq. 32 in Boresch et al. (when using this specific set of restraints). The formula to use is the following, but it is suggested to first read the relevant paper to better understand where it comes from.

[math]\displaystyle{ \displaystyle \Delta G^{solv}_{restr\_on} = RT \ln\Bigg[ \frac{8 \pi^{2}V^{0}}{r_{0}^{2} sin \theta_{A,0} sin \theta_{B,0}} \frac{(K_r K_{\theta_{A}} K_{\theta_{B}} K_{\phi_{A}} K_{\phi_{B}} K_{\phi_{C}})^{\frac{1}{2}}}{(2 \pi k T)^{3}}\Bigg] }[/math]

Where:

[math]\displaystyle{ R }[/math] is the ideal gas constant;

[math]\displaystyle{ T }[/math] is the temperature in Kelvin;

[math]\displaystyle{ V^{o} }[/math] is the volume corresponding to the one molar standard state (1660 Å[math]\displaystyle{ ^{3} }[/math]);

[math]\displaystyle{ r_0 }[/math] is the reference distance for the restraints;

[math]\displaystyle{ \theta_{A}, \theta_{B} }[/math] are the reference angles for the restraints;

[math]\displaystyle{ K_x }[/math] is the force constant for the distance ([math]\displaystyle{ r_0 }[/math]), two angles ([math]\displaystyle{ \theta_{A}, \theta_{B} }[/math]) and three dihedrals ([math]\displaystyle{ \phi_{A}, \phi_{B}, \phi_{C} }[/math]) restraints we applied.

You can use the restraints.py script provided to get the results of this equation (the values of the input variables, corresponding to the restraints defined in the topology, have already been set in this case, but you will need to change these if you use different equilibrium values or force constants). If you are using exactly the set of restraints provided with the input files, this should give 6.906 kcal/mol for turning the restraints on (-6.906 kcal/mol for turning them off, i.e. going from state C to B in the thermodynamic cycle). Note that the formula also contains the standard state correction.

Final Results

Now it is possible add all contributions to recover the binding free energy:

[math]\displaystyle{ \Delta G^{o}_{b} = - \Delta G^{prot}_{elec+vdw+restr} + \Delta G^{solv}_{elec+vdw} + \Delta G^{solv}_{restr\_on} }[/math]

Note that since we calculated the free energy difference for the decoupling (state F -> D) of the ligand from the complex, we now take its opposite. Based on the results mentioned above, I obtained:

[math]\displaystyle{ \Delta G^{o}_{b} = (-21.192 \pm 0.044) + (7.739 \pm 0.021) + 6.906 = -6.547 \pm 0.049 }[/math] kcal/mol

where the uncertainties have been compounded as the root sum square [math]\displaystyle{ \sqrt{\sigma_1^2+\sigma_2^2} }[/math], since they are for two independent free energy estimates.

The published result for this binding free energy was of -6.09 kcal/mol, which is not far from what obtained here, considering also the use of a different Gromacs version and slightly different setup/options (see Note 2 for a brief comment on the treatment of long-range LJ interactions). Also consider that only 1 ns of sampling per window was used. Running the whole calculation three times, it is possible to get a better idea of the precision of the setup; doing this I obtained the following mean and standard deviation:

[math]\displaystyle{ \Delta G^{o}_{b} = -6.38 \pm 0.26 }[/math] kcal/mol.

Which includes the published result within about 1.1 standard deviations.

Notes

1) If you would like to use Hamiltonian Replica Exchange (HREX), you can simply add the -replex and -nex flags to mdrun when running the production simulations, after having already run all minimisations and equilibrations. The -multidir flag can be used to tell Gromacs where to find the .tpr file for all windows to be run in parallel.

   mdrun -multidir lambda.*/PROD/ -s prod.tpr -deffnm prod -replex 1000 -nex 1000000

Here are the results I obtained by using HREX rather than separate simulations: HREX Results. If you compare the O_MBAR matrix obtained with HREX to the one obtained without it, you can see how using HREX resulted in better phase space overlap between states.

2) Boyce et al. applied a long range dispersion correction called EXP-LR to their final results. The EXP-LR method is described in Shirts et al., J. Phys. Chem. B, 2007. What it does is basically correcting for the fact we are using a cutoff for the van der Waals interactions in a nonisotropic system. In the input files provided, however, the LJ-PME method was used for the treatment of the vdW interactions. Thus, the long-range part of the vdW interactions has already been accounted for directly during the simulations. In your calculations, you do not necessarily have to use LJ-PME, as it comes at additional computational cost. If you prefer, you can use the EXP-LR correction instead, or no correction at all. Taking the long-range LJ interactions into account properly will however make the results you obtain more reproducible, as they will not depend on the exact cutoff value chosen. In the old tutorial for Gromacs 4.6 you can find an explanation on how to obtain the EXP-LR correction. I would suggest to read the original paper first though.